PMwG Log-Likelihood Functions
A blog post to help with writing log likelihood functions to be used in PMwG. The examples shown in the PMwG Sampler Doc are quite specific, and so this blog aims to outline the general process of constructing a likelihood function. This blog is probably most useful for anyone who is looking for more info on how to make these functions for different RT models, or any general probability based hierarchical models. Probability based modelling involves working out the probability of some data given a model (and certain model parameter values). This could be evidence accumulation models, signal detection theory models, categorisation models and many, many more.
To get started with PMwG, you’ll need some data - which can be any shape and can take any values, as long as there is a subject column which identifies the separate subjects - and a likelihood function - which calculates the likelihood of data given some parameter values. The data can be small or large, but should have multiple entries per person. Further, the data should be able to be split be subject column (i.e. subject_i <- data[data$subject==i,]) and will link closely to the structure of the likelihood function. For example, in the SDT example in Chapter 2, the data for the fast likelihood shows 16 possible values for each participant, which counts the number of responses in each cell of the design. In the likelihood function in Chapter 2, probability is calculated for each response type and is multiplied by the number of these responses (from the column n). This shows that the data can take any form, as long as it is accounted for in the function.
Writing Log-Likelihood Functions
Overview
PMwG is a Bayesian hierarchical model sampling method proposed by Gunawan et al., (2020). In our PMwG sampler documentation, there are several examples of (and countless references to) writing your log likelihood function. For anyone new to modelling, or just new to this style of modelling, this step is the equivalent of STAN and JAGS model.text files. The way these operate though is vastly different.
The main purpose of the log likelihood function, which I’ll refer to as LL from here on, is to return a single logged likelihood value. This value can be thought of as a probability, or marginal likelihood, of some data given some model parameters under this model. If this stuff and modelling is all pretty familiar to you, you can skip straight to the “How to Make Your LL function” section.
NOTE: For people new to this kind of modelling, by sampling, here I mean “training” your model on the data. This is done in a Markov Chain Monte-Carlo (MCMC) kind of way for PMwG, where values are selected when they are good on each iteration, until the model is trained to be in the best place. We call it “sampling” as we are sampling the parameter space (i.e. all possible values of parameters), of which we need many plausible values at the end so that we can process these in post (i.e. essentially if we only get one “sample” of parameters, we restrict ourselves, sampling lots of good values allows us to see the variance and do more accurate posterior calculations). Later on, after the model is trained, we may do anpother type of sampling where we sample “posterior predictive data” - i.e. we use the trained model parameters to generate data. For this second kind of sampling, I’ll try and refer to it as “generating”.
Usually, for data, we can easily return the density of a value given some input. For example, if I’d like to know the probability of a response coming from a certain normal distribution, i could do;
value <- 3
m <- 4 #mean
s <- 0.5 #standard deviation
dnorm(x=value, mean=m,sd=s, log=FALSE) #density function
## [1] 0.1079819Which returns a probability value. Plotting this shows us a little bit more;
ggplot(data = data.frame(x = c(2, 6)), aes(x)) +
stat_function(fun = dnorm, n = 101, args = list(mean = 4, sd = 0.5)) + ylab("") +
theme_bw()+geom_vline(xintercept=3, colour="red")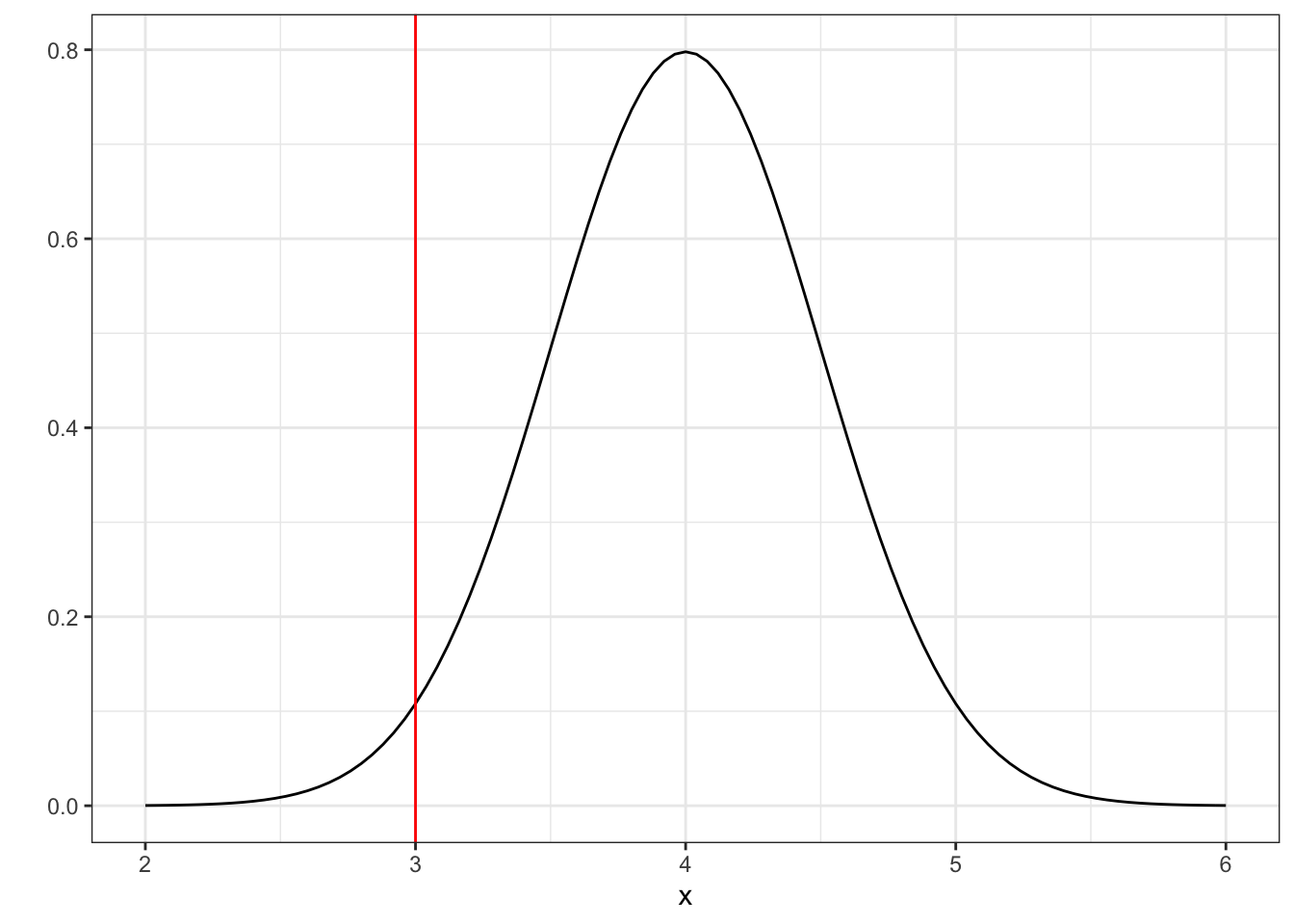
And so this looks about right. There’s a 10% chance this response is under this distribution. So now we know that we can get the density of data for values. If i change log to TRUE, i get the log likelihood for these parameters and the data point I have. Lets see what this would look like;
dnorm(x=value, mean=m,sd=s, log=TRUE)
## [1] -2.225791For PMwG we need to return the log-likelihood so that the values are useful to the algorithm. This also means we can add values together rather than multiplying probabilities together - and this protects against tiny values.
In a modelling scenario, we would repeat this density calculation many times (i.e. for each data point). But what if there were two conditions, which differed for the mean of the distribution? The distributions might be hypothesized to look like this for example;
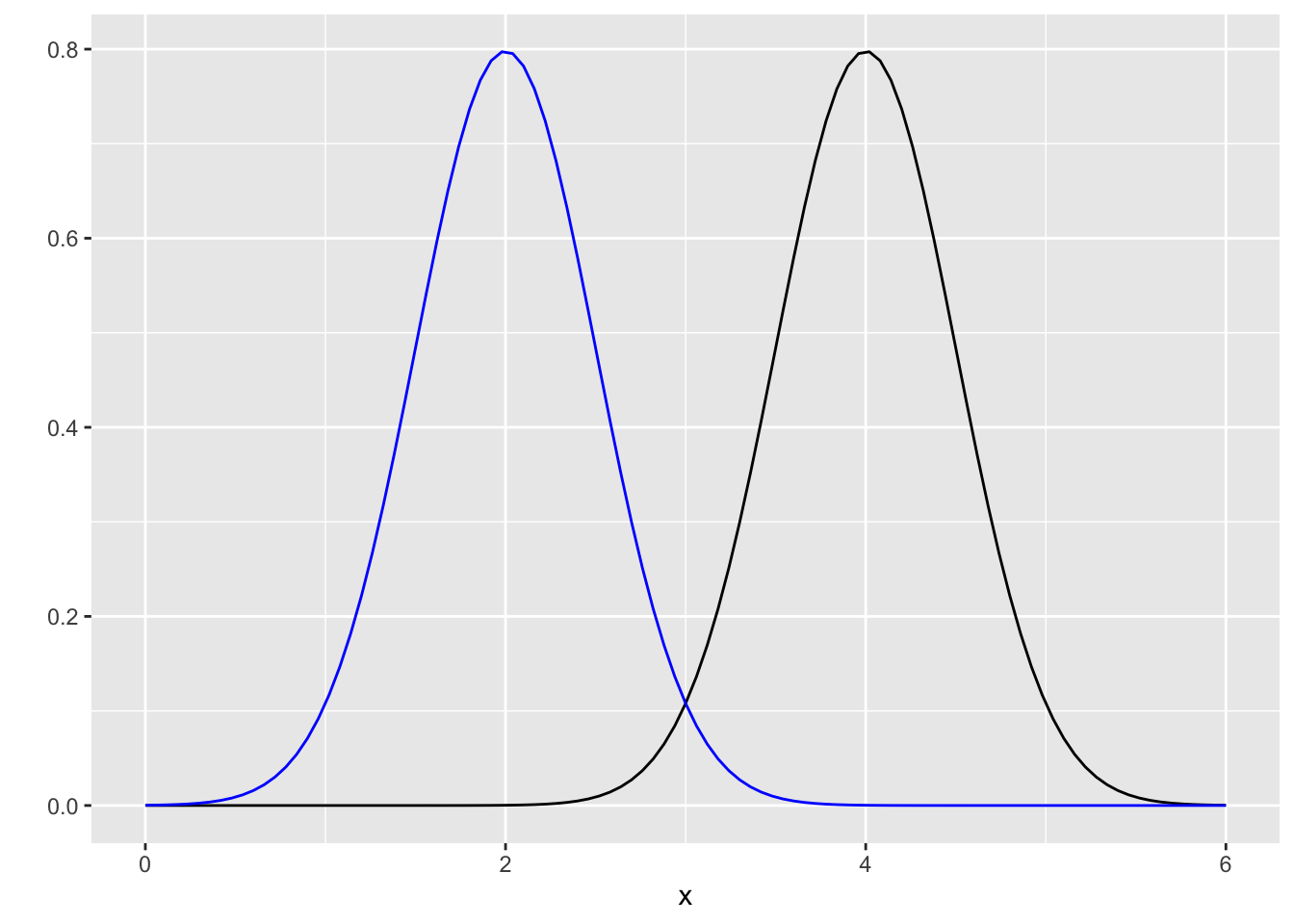
Now we can check different data points for different conditions. Lets imagine a person’s responses in condition 1 were 4, 3 and 3.5 and in condition 2 were 2, 2.1 and 4. Using the same method as above, we can calculate the probability of these responses (data) given some parameters (here, the parameters are the mean and standard deviation, but we only vary the mean).
values_1 <- c(4,3,3.5) #data for condition 1
values_2 <- c(2,2.1,4) # data for condition 2
m1 <- 4
m2 <- 2
s <- 0.5
cond1 <- dnorm(x=values_1, mean=m1,sd=s, log=FALSE)
cond2 <- dnorm(x=values_2, mean=m2,sd=s, log=FALSE)
cond1
## [1] 0.7978846 0.1079819 0.4839414
cond2
## [1] 0.7978845608 0.7820853880 0.0002676605So we can see here that the two means we’ve proposed are pretty good guesses for the probability of these responses. In the PMwG algorithm, each particle proposes new guesses for the parameters for each subjects’ data. These values are then input into the model (similar to above), and then the sum of these logged values is returned. The particle with the highest log likelihood is chosen on each iteration so that eventually, the best parameter values are chosen for each subjects’ data.
The model above is a model that assumes that responses come from normal distributions which may differ across conditions. If there was no difference in conditions, then PMwG would likely return equivalent mean parameter values (m1 and m2). This is a simple model, and so there is much more complexity to add before reaching a full drift diffusion or LBA model. In the next section I outline some considerations for modelling and then steps to creating your likelihood function.
Linking Models and LLs
It’s important to note here about how LLs and models link. You may think the LL is the model, and it kind of is. We use the LL function to estimate the likelihood under the model - that’s pretty clear from above. So how do I fit my model in? Well this comes in the call to the density function (like dnorm or dLBA). Many density functions for probability models already exist in a variety of packages. These functions are often detailed in papers, and so if a density function does not exist, you can still easily calculate the density for models given these equations in papers – although it is likely someone has already done this for you. If a density function does exist, this is usually as easy as inputting the observations (data) and the parameter values. For some examples of this see the rtdists package
What’s the purpose of modelling your data?
The first question to ask is “what’s the purpose of modelling my data?” or “what should the modelling tell me about the data?”. There are many different flavours of answers to this question which should be considered from the outset of any experiment/modelling exercise. These ‘flavours’ fall into several main categories.
- selective influence
- model comparison
- comparing groups
- finding the ‘best’ model
Selective influence
Selective influence is a manipulation used to check whether a parameter maps to the appropriate parameter. For example, in a model where a parameter was thought to map to memory strength, then values for this parameter should be higher in conditions where memories are stronger or more deeply encoded (and not other parameters of the model). This is a type of experiment we do to test the validity and reliability of our models to make sure that they capture the effects we are interested in.
Model comparison
Model comparison is a highly common practice in statistical methods which involves comparing different model accounts of the data. In the PMwG documentation, we briefly touch on how to compare models and different comparison methods. For the purposes of writing an LL however, this often involves writing several different LLs which vary (in parameters or models used) and running them separately. The results from these are then compared in model comparison methods. An example of a model comparison could be from the above example, where we might compare the descriptive adequacy of normal distributions to truncated normal, uniform distributions, log normal and exponential distributions to decide which best describes the data.
Comparing groups
Comparing groups is highly important for psychology and other sciences, especially in modelling exercises, as we may wish to discover how groups differ in underlying parameters or even if they differ. There are many varying ways of doing this. In PMwG we can do between-subjects model fits or we may run the models separately for the different data sets and compare parameter outputs.
Finding the ‘best’ model
Similar to model comparison, finding the best model is often done when researchers aim to describe certain behavior or data. In finding the best model, one may avoid fitting the full model space so as to reduce the complexity (and not limit flexibility) of models. After this, complexity may be added in to capture more of the data. This is often done by fitting a model, checking the model to see how well it did, and then adding in parameters or complexity to see if this can help improve the model fit. This can also grow into a model compariosn exercise, where the models to compare do not cover the full model space.
So what’s the point?
Evidently, there are many different methods for modelling that achieve different outcomes, and this can influence how we construct our LLs. For now though, we’re going to stick with the “finding the best model” approach.
Which model will capture the effects?
So now you have the purpose of your model, you need to ask what kind of model will capture the effects. In most of the research I do, I’m working with response times and decision making, so I work with evidence accumulation models. For these models, I’m lucky because the density functions are already written. For many applications this is the case, although in some, you may have to put in some extra effort to write your own density functions.
The effects you’re looking at are important for considering what models you’ll use. Being in your field, you’ll probably already know an array of different models that exist and are evidence based that you will want to fit. But for now, lets go through some key considerations.
What type of model is needed to answer the purpose?
In the example I gave above about model comparison, I talked about comparing different distributions. For the purpose of this question (i.e. what distribution do these responses come from), then these models (i.e. different distributions) answer the purpose. For a question where I wanted to know where people set their mean and sd given I think the distribution is normal - this would require only a normal distribution and looking at the PMwG parameter estimates.
In an evidence accumulation model, I may want to know about start point variability or within trial drift variability, and so it is better for me to use the DDM rather than LBA, as these parameters are not evaluated by the LBA. Put simply, make sure the model you use answers the purpose you set out to achieve.
Is this model flexible for my effects?
Secondly, it’s important to consider the flexibility of the model and whether the model will allow you to capture effects. For example, fitting an exponential curve to data could really restrict the space I’m sampling (i.e. positive only and exponential values), and may bias models towards inflated values which don’t capture the true tails of the distributions of my responses. Obviously this is an extreme example, but this needs to be considered when planning which model to use.
Is your data suitable?
The next consideration is with your data. This should probably come earlier, or even before the experiment has been done. Remembering that PMwG is for hierarchical modelling, which means we get both group and individual level parameter estimates. If we wanted to estimate means and standard deviations for the top example, this would work fine - we could collect lots of data from a large sample and then see how individuals set their means (and sd’s) for the two conditions. This would give us both individual estimates, but also will allow us to see group level estimates.
However, if we take only one data point per person and randomly allocate people to conditions, this causes trouble. First of all, at the individual level, we will not have enough data to fit models. Secondly, for the m1 and m2 parameters, people would be missing values, and so this estimated value would revert to the prior, thus being uninformative at individual subject level and less useful at the group level. Evidently, we need to collect enough data to fit our models, but also consider our experimental manipulations - ensuring we have enough data in each cell of the design. This extends to the type of design, where between-subjects effects become difficult to account for. This can be done, but experimental rigor is sacrificed as it either requires separate fitting or uninformed random effects.
What will the models priors be?
Finally, it’s important to consider priors. PMwG uses a multivariate normal prior (and Huang and Wand’s (2013) prior on the variance). This isn’t super important for using the sampler, but is important to the methodology. What’s important for using the sampler, is that you specify the prior mean and mean variance (remembering this is on the real number line). For most models we do, we generally set the mean at 0 and the variance at 1, but this may be too restrictive for some models. Further, you should consider parameter transformations you may undertake and how these parameters will appear before they are transformed. For example we usually take the exponenital of input parameters in LBA modelling to ensure they’re strictly positive, this means the exp of 0 is 1, and such our prior within the model is 1. This is also the case for variance, where the exponential of -1 is 0.37 and the exponential of 1 is 2.72 which would be the case for one standard deviation either side of the mean in this example.
An example of these priors are shown below;
priors <- list(
theta_mu_mean = rep(0, length(pars)),
theta_mu_var = diag(rep(3, length(pars))))
What are the important effects?
So we now know our purpose and we’ve chosen a model to fit. Next things to consider are the effects. Most of the time, you’ll know the effects you’re interested in because these will form the research questions and will be evident from descriptive statistics. These are effects like condition 1 vs condition 2 from our top example, but could also be related to stimuli, responses and more. Lets go through some key considerations when designing the LL and the experiment.
Experimental manipulations?
- What were the manipulations in the experiment?
- Were these between or within subjects?
- What would we actually be looking for in the data (i.e. differences in response times, accuracy, choice proportions etc)?
How do manipulations manifest?
From these experimental manipulations, we need to consider how these might manifest in the cognitive model. In a cognitive model, the parameters relate to underlying cognitive processes or representations. Consequently, we should propose models, and parameterisations, that relate to our experimental conditions. This might mean that in a 3 parameter model for a 3 condition experiment, we could have up to 9 parameters (or more if there was added model complexity), where for each condition, the model has 3 unique parameters. We also might hypothesize that in the 3 parameter model for the 3 condition experiment, that 1 parameter is fixed across conditions, while the other two vary. Comparing the 9 parameter model to the 7 parameter model (and other combinations) becomes a model comparison question.
Working out how these manipulations may manifest is highly important in modelling – both going forward and looking back. For example, when planning an experiment that involves modelling, one should consider the type of modelling question and the best experimental manipulation to implement to answer this question. When planning LLs, one should consider how the experimental manipulation would logically, and rationally, map to parameters. This is not only important for the model, but is vital for drawing clear conclusions.
Group differences
It’s also important to consider potential group differences when writing LLs. Where group differences exist, we may see the model under-fitting the data, however, including these effects in the LL could lead to uninformed cells in the model. If this is the case, it may be best to run the model separately for the different groups (but this method also has a weakness in that the fits are not informed by one another).
Important effects? Are these present in descriptives? What does the literature say?
If we do expect to see effects of manipulations in the model, we should first check if the effects of manipulations can be seen in the descriptives. It’s important that the manipulation actually worked before we start explaining how/why it worked. This can also be useful to see main and interaction effects which could be important to the model.
Considerations of writing the LL
Finally, we’ve made it to the LL function! You’ve now thought about all components of your data and your experiment (probably). But, before writing this, lets take some time for final considerations.
Consider the stimuli and responses
When considering your stimuli and responses, consider how these may vary across conditions, how these might vary with response types/proportions/biases and what effects these may have on the underlying cognitive process. It is often the case that certain stimuli or responses can lead to inconsistencies in the model (and in the descriptives). Consequently, consider doing a deep dive into the descriptives first up to check for any weirdness - then decide what to do with these. It might also be an idea to run a full model (in addition to other models) to ensure nothing strange is going on in certain conditions or with certain parameters.
Consider your data
Following on from the above, when doing a deep dive into the data, consider cut points for outliers and standardization. As PMwG fits hierarchical models, it is often unlikely that corrections are required (such as logging RTs or minimizing the impacts of extreme data), however, occasionally data may need to be removed, such as for bad participants or lapses of attention (where these aren’t fit by the model).
How to make your LL
In this section, I’ll detail the methods I generally use to make my LL function, and in the next section, I’ll test it. There are six main steps to making a LL.
- Prepare the parameters to be used
- Ensure no bad parameter values
- Map parameters to conditions
- Make the ‘sample’ component
- Make the ‘likelihood’ component
- Return
PMwG samples random values on the real line for the parameters of the model. These values are taken from a distribution of values centered on the group mean or the individual mean, with some variance, in a multivariate normal distribution. So for example, for 3 true parameter values in a model (say -1, 2 and 9), PMwG will propose 3 values as a particle (where we have n particles) for n iterations, constantly returning the most likely combination of parameters. On iteration 1, three values are selected at random (say 0,0 and 0) and a likelihood is returned. On the second step, n particles more values will be proposed using the previous particle as a reference point (from both the group and individuals previous particle) and the winner will be selected (say 0,1 and 5). This process happens over and over until the posterior space is reached.
Prepare the parameters to be used
As PMwG returns values on the real number line, we first have to prepare our parameters to be used properly in the function. This may require corrections, such as taking the exponent of these values (as is done by Gunawan et al., 2020, JMP), converting a number to between 0 and 1 (for probability parameters), or may require a mathematical function, for example, certain parameters may become 1/parameter. This should be done early in the LL.
NOTE: if there are any transformations or corrections carried out, it is important to remember and account for these when evaluating the output and generating posterior predictive data.
ll <- function(x, data, sample=FALSE){
x = exp(x)In this example, and those shown in the sampler documentation, we use an exponential transformation. This is to ensure parameter values are always greater than 0 (as the model doesn’t work if values are below 0). Evidence for this transformation comes from the main PMwG paper by David Gunawan and colleagues (Gunawan, et al., 2020, JMP). It is not always necessary to carry out transformations, however, it is important to consult the literature for advice on general practice (especially keeping in mind that PMwG samples from the real line).
Ensure no bad parameter values
Secondly, to save computation time and protect against bad values, I often include code to exclude ‘bad’ parameters. For example, if specific parameters should be non-negative and a negative value is proposed from the PMwG algorithm, the LL automatically returns -1e10. Example of this is included below.
if (!sample){
if (any(data$RT < x["t0"])) { ### for this example, i need to make sure t0 is not below any RT, if there are RTs below t0, this is bad for the model
return(-1e10)
}
if (x["b"] <= any(abs(c(x["b.1"],x["b.2"],x["b.3"])))) { # for this example, i need to add b.n to b, and so if there are negative b.n's this would make b below 0, which again is bad for the model
return(-1e10)
}
}Here, x is the parameter vector, and the parameters have names such as “b”, “t0”, “b.1” etc. To refer to parameters, I use x[“b”] naming convention. You can also refer to these numerically, such as x[1], however, this is risky and can lead to potential errors. Naming is safer.
I only use this when sample = FALSE, as this can mess up posterior predictive sampling.
It’s important that if the density function cannot handle specific values (i.e. dLBA can’t work with negative values), then this safety check should be put in, so that NAs aren’t returned (which would break the sampling).
Map parameters to conditions
Next up, I need to map parameters to conditions. I referred to this earlier when discussing experimental manipulation effects on the data/model. When I refer to mapping parameters to conditions, this means that parameters which refer to conditions are associated with the correct data. i.e. parameter “b.1” is associated with condition 1 and so fourth. All this step does is ensure that the correct parameter values are input into the model for each data point evaluated.
NOTE: In process models, parameters, like A and B used in the examples below, often refer to specific components. For example, in cognitive modelling, parameter A may refer to the individuals bias in responding and parameter B could refer to the sensitivity of responding. Many models used in cognitive modelling link to specific cognitive processes or structures, and links to these processes are made through selective influence studies. There is often a significant amount of literature justifying parameters in a model and underlying processes these relate to.
When writing your LL you could do parameter:condition associations line by line, and I recommend this at first, or through vectorising or other methods. The line by line method is slow, but also more accurate. Later on you can move to more advanced methods which quickly loops over conditions. Note that the more calls you make to the density function, and the more loops in the function, lead to more time.
I’ve included two examples below of mapping parameters to conditions, in both slow and fast ways. The slow way is computationally inefficient, but is quite safe. The fast way is fast, but risks parameters not mapping as effectively. You should write your function in both ways, then compare them to ensure the output is the same and correctly mapping. For more info on this, see here
Slow
parameter.b = parameter.A = numeric(nrow(data)) # first i create a vector to store the values in
parameter.A = x["A"] #here A is the same across conditions, so i store A in here
for (i in 1: nrow(data)){ #here i loop across rows to see which condition the data relates to and store the appropriate parameter for that row - either b.1 or b.2
if(data$condition[i]==1)
parameter.b[i] <- x["b.1"]
} else if(data$condition[i]==2) {
parameter.b[i]<- x["b.2"]
}
Fast
parameter.b = parameter.A = numeric(nrow(data)) # first i create a vector to store the values in
parameter.A <- x["A"] #here A is the sham across conditions, so i store A in here
parameter.b <- x[c("b1", "b2")][data$condition] #here i do the same as above, in a faster way.
Evidently, there are many ways of doing this to make this operation more computationally efficient. You may also find you need to call the density function several times (i.e. density for one subset of data, and then for another or even in a line by line way), however, the less calls the better (faster). Also, you may find that you have main and interaction effects in the model, these are fine too, and there are many ways of implementing this, but need to be closely checked. Examples of this can be seen below.
In sum, for each trial, we need to ensure that the call to the density function is referring to the correct parameter values.
main and interaction effects
In this example code snippet below, I show slow and fast ways for mapping out parameters across conditions. Here, this model includes all types of effects (similar to that in an ANOVA), where each cell of a design contains a parameter. This could also only look at main effects (i.e. only b.1 and b.2 and only slow and fast without having the interaction) or could include some interactions in addition to the main effect. This becomes particularly important in designs with more experimental factors.
Slow
parameter.b = parameter.A = numeric(nrow(data)) # first i create a vector to store the values in
parameter.A = x["A"] #here A is the same across conditions, so i store A in here
for (i in 1: nrow(data)){ #here i loop across rows to see which condition the data relates to and store the appropriate parameter for that row - either b.1 or b.2
if(data$condition[i]==1)
if(data$speed[i]=="slow"){
parameter.b[i] <- x["b.1.slow"]
} else if(data$speed[i]=="fast")
parameter.b[i] <- x["b.1.fast"]
} else if(data$condition[i]==2) {
if(data$speed[i]=="slow"){
parameter.b[i]<- x["b.2.slow"]
} else if(data$speed[i]=="fast"){
parameter.b[i] <- x["b.2.fast"]
}
}
Fast
parameter.b = parameter.A = numeric(nrow(data)) # first i create a vector to store the values in
parameter.A <- x["A"] #here A is the same across conditions, so i store A in here
for (cond in unique(data$condition)){
for (speed in unique(data$speed)){
parameter.b <- x[paste0("b",cond,speed)]
}
}
Again, this can be done in a variety of ways, but does require thorough checking to ensure parameters map correctly and effects carry.
Point/intercept method
Another method for dealing with main and interaction effects is with a “point-intercept” method of parameter mapping. We often use this method to limit the number of parameters when the parameter space is growing. This method is similar to a treatment effect method used in many ANOVA analyses. This is referred to above when I allude to main and interaction effect parameters.
For the point intercept method, there is a grand mean. For each specific condition, the parameter becomes the difference from the grand mean parameter. This means in our parameters, we have a grand mean parameter and a difference parameter. In the example above, the parameterisation is too simple, so lets look at two examples from the PMwG Doc in Chapters 2 and 3.
In Chapter 2, an SDT model is used. For the parameterisation, the d’ is the difference between parameters. We could estimate a mean for non-targets, a mean for targets and a mean for lures. However, these values are arbitrary and so could move along the scale unconstrained. Instead, we set the mean of non-targets to 0. We then only need to calculate the distance (d’) from non-targets to lures and from non-targets to targets. So lets start with targets, we call this parameter d’. Then, all we need to do is add a d’ increment to the lures parameter (i.e. d’ + d’ increment) to get the mean. These parameters are all on the real line, and so the d’ increment could be negative, allowing the mean for lures to fall anywhere on the line.
Secondly, in chapter 3, we use an LBA model. In this example, we could parameterise in a way where we have a grand mean for threshold with differences for the conditions. This means that threshold is constrained by the mean parameter, and then for the other parameters, we add an increment to see differences between conditions. This is especially useful if we had bias in responses, where threshold for left was different than threshold for right responses. In this example, we could do this;
bL=bR=numeric(nrow(data))
for (cond in unique(data$condition)){
bL<-x["b.mean"]+x[paste0("b."), cond]
bR<-x["b.mean"]-x[paste0("b."), cond]
}
In this example, the x[“b.i”] parameters need to be on the real line so that they can move the bias up or down for either responses (in each condition). This means that we should not take the exponential of these specific parameters at the start of the LL.
NOTE: This kind of function would also require a check so that the overall threshold parameter (after adding/subtracting the difference) couldn’t be negative, and so something like the below is needed;
if(!sample){
if (x["b"] <= any(abs(c(x["b.1"],x["b.2"],x["b.3"])))) {
return(-1e10)
}
}Make the ‘sample’ component
Next up, we make the sample function for when sample = TRUE. This is not essential for PMwG to work, but does make post-processing much easier. In this step, we use the parameters above to create data with random generation functions (such as rnorm, rbinom or rLBA). This generally requires one call to a random generation function with the parameters created above. We usually do this as a loop over rows to protect against any weirdness from the generating function. This is slower, but safer (and is only called a handful of times).
data$rt<-NA
for (i in 1:nrow(data)){
tmp <- rpackage::rfunction(n=1, A = parameter.A[i], b = parameter.b[i]) ## rpackage::rfunction could be for example rtdists::rLBA
data$rt[i]<-tmp
}
Make the ‘likelihood’ component
Next up, we make the density function for when sample = FALSE. This IS essential for PMwG to work. In this step, we use the parameters above to obtain the probability of each data point for the given parameters. This means that following the parameter specifications above, the density for data from trial i is calculated under the correct parameter inputs (i.e. parameter.A[i] and parameter.b[i]). So on each trial, we should see density[i] (of data[i]) = model_function(b=parameter.b[i], A=parameter.A[i]).
Evidently, you could do this as a loop over rows, however, most density functions allow you to specify vectors of data and parameters (which is what we created above). The likelihood is generally obtained through density functions (such as dnorm, dbinom or dLBA), however, you may need to specify your own depending on the model.
out <- numeric(nrow(data))
out <- rpackage::dfunction(data=data$rt, A = parameter.A[i], b = parameter.b[i]) ## rpackage::dfunction could be for example rtdists::dLBA
}
Usually, density functions already exist or are pre-specified - many R packages are available for these. If a density function does not already exist, you probably have a mathematical model in mind. It’s important that this is tractable and able to recover effectively.
Return
Finally, you need to return the likelihood (or randomly generated data). If you have multiple probabilities, this will require combining these. We generally do this through;
if(!sample){
return(sum(log(out)))
}
Although occasionally, you may want to protect against really small values, and so we do;
bad <- (out < 1e-10) | (!is.finite(out))
out[bad] <- 1e-10
out <- sum(log(out))
or;
return(sum(log(pmax(out,1e-10)))
For returning data when sample = TRUE, you should write your sample function similar to above to ensure that the generated data is returned (not the original data). Then, we just need to return data;
if(sample){
return(data)
}
WARNING: if you return data, you need to ensure that this is only when sample = TRUE and - for a posterior generating function to work - must replace the values in the actual data. For more on simulating from the posterior, see here
Full function
Shown below is how your full likelihood function will look;
(NOTE: this won’t work because it’s all example text)
LL <- function(x,data,sample=FALSE){
#note, x is a vector of named parameter values
# data is data - but in pmwg will be data for each subject
#sample = FALSE should be default. if true, uses x to randomly generate. If false, uses x for density.
#transform vector of parameters
x<-exp(x)
#map
parameter.b = parameter.A = numeric(nrow(data)) # first i create a vector to store the values in
parameter.A <- x["A"] #here A is the same across conditions, so i store A in here
for (cond in unique(data$condition)){
for (speed in unique(data$speed)){
parameter.b <- x[paste0("b",cond,speed)]
}
}
#generate
if(sample){
data$rt<-NA
for (i in 1:nrow(data)){
tmp <- rpackage::rfunction(n=1, A = parameter.A[i], b = parameter.b[i]) ## i.e. rtdists::rLBA
data$rt[i]<-tmp
}
#return
return(data)
} else{
#checks
if(!sample){
if (any(data$RT < x["t0"])) {
return(-1e10)
}
}
out <- numeric(nrow(data))
out <- rpackage::dfunction(data=data$rt, A = parameter.A[i], b = parameter.b[i]) ## i.e. rtdists::dLBA
return(sum(log(pmax(out,1e-10)))
}
}
Testing your LL function.
Finally, it’s REALLY important to test your likelihood function. In this section, I’ll go through a couple of methods I’ve given titles to.
Line by line testing
For this method, first make some x values, for example;
pars<- c("A","b.1","b.2") #names of params
x <- c(1,0.5,0.7) #make sure you give different conditions different values so they don't all look the same and its confusing.
names(x)<-pars
From here, use this x and your data (or a subset) to work through each line of the function. What you should see is values for the correct parameters mapping to the correct conditions in your vector (for example x[“b.1”] matches with data that is from condition 1 etc). In our example above, parameter.A will be a vector of 1’s (x[“A’]=1) and parameter.b will be a vector of 0.5’s and 0.7’s which match to data$condition.
From here, work through your LL running each line (or loop) of the function to ensure there are no errors, values map correctly, and the density function works correctly. This means that parameter vectors should use the correct conditions and values and output as expected.
Alternate input values
On the topic of density functions working correctly, this is the next step. For this step, again, create some parameter values. Then just run your LL with these values and data. Then, make some new parameter vectors, and repeat. What we should see is that;
- the likelihood changes with different input values
- the likelihood changes in the right direction (i.e. for silly parameter values, a low likelihood is returned)
- the likelihood should quickly return bad likelihood for bad parameter values (as discussed above)
This is a quick and easy test that can be done many times and should give you some idea of whether your likelihood is ‘working’. There are more thorough and robust checks shown in Chapter 3 of the sampler doc, but this is a good first pass.
Profile Plots
Another strong way to test the likelihood is with profile plots. This is a basic kind of simulation and recovery exercise where we first generate some data using the sample = TRUE argument and then test different values using the sample = FALSE argument. Here, I use a function from the PMwG Toolkit to make my profile plots.
#### profile plot function
#### Contributed by Reilly Innes
#### Use pwmg_profilePlot on an initiated PMwG object to ensure your likelihood functions correctly
#### This function takes in the initial theta_mu estimates and simulates a small amount of data based on these
#### plots are returned which show how the likelihood changes as the generating value changes
#### For the different generating values, we use small increments (which can be negative or positive)
#### We expect to see inverse U shaped curves, where the likelihood is most likely at the generating value and falls away as we get further from the generating value
#### NOTE: The likelihood function needs both sample = TRUE and sample = FALSE arguments to function correctly
#### Also, avoid putting protective statements (like if(any(data$rt)<t0) etc) at the beginning of the function
#### These statements should go in the if(sample=FALSE) part
require(ggplot2)
require(tidyr)
## Loading required package: tidyr
require(pmwg)
## Loading required package: pmwg
pmwg_profilePlot = function(sampler, generating_values=NULL){
if(is.null(generating_values)){
#create generating values based on theta_mu
generating_values <- sampler$samples$theta_mu
names(generating_values)<- sampler$par_names
} else{
names(generating_values)<-sampler$par_names
}
#make the test data set. here I use a tenth of the total data for speed
test <- sampler$ll_func(x = generating_values,
data = sampler$data[c(1:(nrow(sampler$data)/10)),],
sample = TRUE)
# this is the number of values to test and plot.
n_values <- 9
tmp <- array(dim=c(n_values,sampler$n_pars))
#here i make the increment, however, you may wish to make this smaller or larger.
#the increment here goes from theta_mu - .2 to theta_mu + .2, with n_values length
increment<- seq(from=-.2, to=.2, length.out = n_values)
for (i in 1:sampler$n_pars){
for (j in 1:n_values){
#need to use all generating values except the current parameter being tested
test_values <- generating_values
#here we change the current parameter by adding the increment
test_values[i] <- generating_values[i] + increment[j]
#test the likelihood given these new values and the test data
tmp[j, i] <- sampler$ll_func(x = test_values, data=test, sample=F)
}
}
#prepare output for plotting
colnames(tmp)<-sampler$par_names
tmp<-as.data.frame(tmp)
tmp <- tidyr::pivot_longer(tmp, everything(), names_to = "pars", values_to = "likelihood")
tmp$increment <- rep(increment, each=sampler$n_pars)
### next, plot these values for each parameter
ggplot2::ggplot(tmp, aes(x=increment, y= likelihood))+
geom_point()+
geom_line()+
facet_wrap(~pars, scales = "free")+
theme_bw()+
geom_vline(xintercept = 0, color="red", alpha = 0.3)
}
For this function, it is essential that both components of the likelihood (sample=TRUE and FALSE) work correctly. This means that parameters are first transformed and mapped before being used by each component. It also means any protective statements are limited to the sample = FALSE section. The function then takes in an initialised PMwG object (from the init function in PMwG - although you can also use a sampled object). Now let’s test this out with a simple LBA example from Forstmann (2008).
data<- forstmann
data$condition <- as.factor(data$condition)
lba_loglike <- function(x, data, sample = FALSE) {
x <- exp(x)
bs <- x["A"] + x[c("b1", "b2", "b3")][data$condition]
t0 <- x[c("t0.1","t0.2","t0.3")][data$condition]
out <- nrow(data)
if (sample) {
data$rt=NA
data$resp = NA
for (i in 1:nrow(data)){
out <- rtdists::rLBA(n = 1,
A = x["A"],
b = bs[i],
t0 = t0[i],
mean_v = x[c("v1", "v2")],
sd_v = c(1, 1),
distribution = "norm",
silent = TRUE)
data$rt[i] <- out$rt
data$resp[i] <- out$resp
}
return(data)
} else {
if (any(min(data$rt) < c(x["t0.1"], x["t0.2"], x["t0.3"])) ) {
return(-1e10)
}
out <- rtdists::dLBA(rt = data$rt,
response = data$resp,
A = x["A"],
b = bs,
t0 = t0,
mean_v = x[c("v1", "v2")],
sd_v = c(1, 1),
distribution = "norm",
silent = TRUE)
bad <- (out < 1e-10) | (!is.finite(out))
out[bad] <- 1e-10
out <- sum(log(out))
return(out)
}
}
# Specify the parameters and priors -------------------------------------------
# Vars used for controlling the run
pars <- c("b1", "b2", "b3", "A", "v1", "v2", "t0.1","t0.2","t0.3")
priors <- list(
theta_mu_mean = c(0,0,0,0,1,1,-3,-3,-3),
theta_mu_var = diag(c(1,1,1,1,2,2,0.1,0.1,0.1))
)
# Create the Particle Metropolis within Gibbs sampler object ------------------
sampler <- pmwgs(
data = data,
pars = pars,
prior = priors,
ll_func = lba_loglike
)
start_points <- list(
mu = log(c(1,1,1,1,2,3,0.07,0.08,0.09)),
sig2 = diag(rep(.1, length(pars)))
)
sampler <- init(sampler, start_mu = start_points$mu,
start_sig = start_points$sig2, display_progress = FALSE, particles = 250)
pmwg_profilePlot(sampler)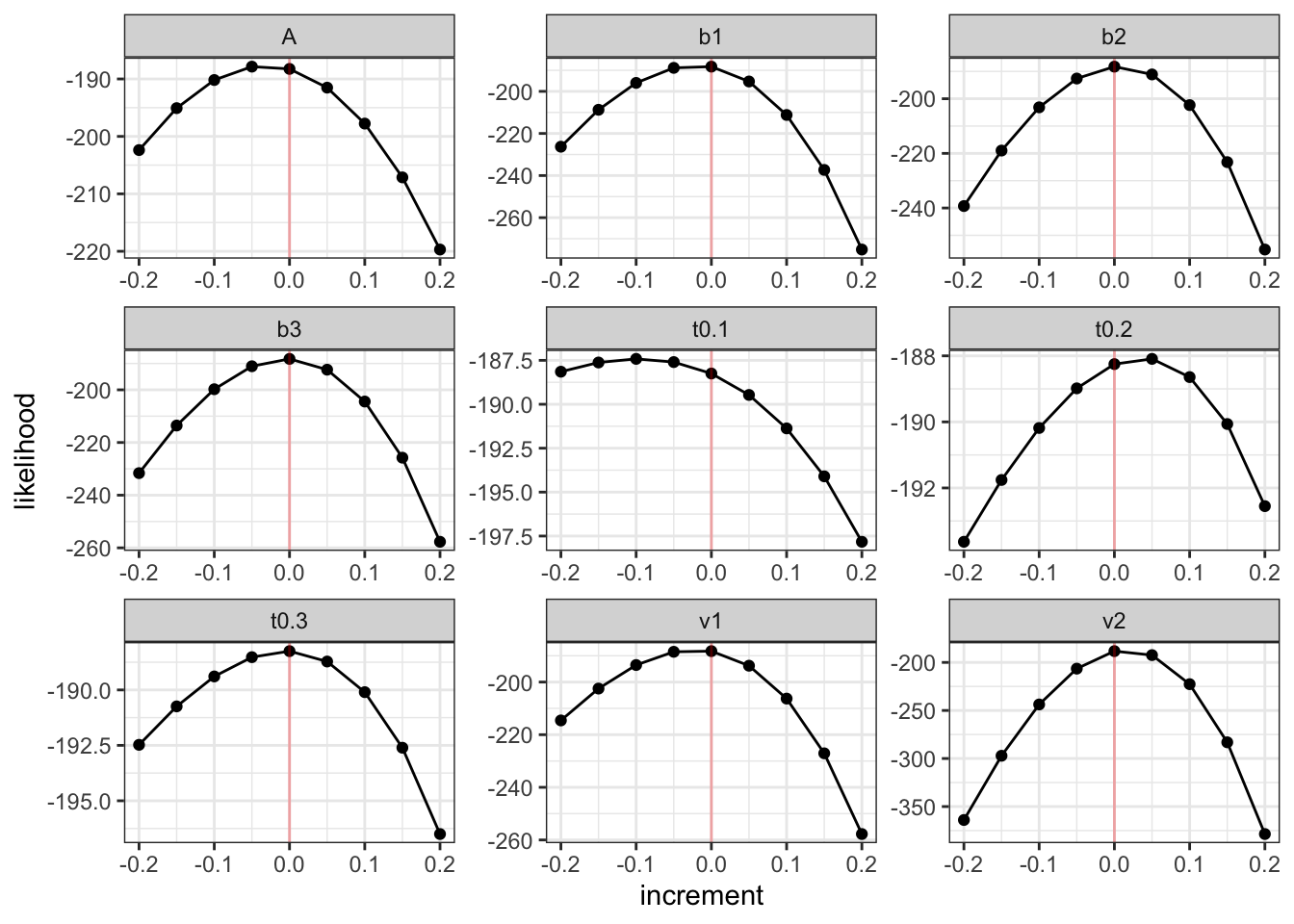
From these plots we can see that for most of the parameters, there is a nice inverse U curve, which centers at 0 increment. This means that the generating value is also the most likely value for that parameter. This indicates that the parameter values simulate and recover well and our likelihood seems to function correctly. If you see different patterns, try using sensible start points or check line by line what could cause the function to return weird values (this could be due to one of the protective statements or could be due to parameters not mapping correctly).
References
Gunawan, D., Hawkins, G. E., Tran, M. N., Kohn, R., & Brown, S. D. (2020). New estimation approaches for the hierarchical Linear Ballistic Accumulator model. Journal of Mathematical Psychology, 96, 102368.
Huang, A., & Wand, M. P. (2013). Simple marginally noninformative prior distributions for covariance matrices. Bayesian Analysis, 8(2), 439-452.